Długość odcinka w układzie współrzędnych

Jak to zrobić

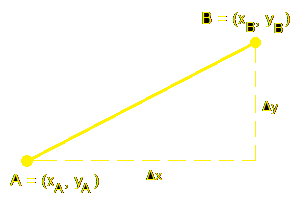
Chcemy obliczyć odległość między punktami AB (długość odcinka AB). Możemy dorysować pionowy i poziomy odcinek, aby powstał trójkąt prostokątny.

Jeśli znamy współrzędne punktów A = (x_A, y_A) i B = (x_B, y_B), to obliczamy jaka jest różnica między punktami w poziomie: Δx = x_B - x_A, a jaka w pionie: Δy = y_B - y_A. Następnie obliczamy odległość między punktami (długość odcinka AB) korzystając z twierdzenia Pitagorasa:

(AB)² = (Δx)² + (Δy)²

Przykład

Oblicz długość odcinka KL, jeśli K = (-3,7) ora L = (4,8)

Δx = 4 - (-3) = 7

Δy = 8 - 7 = 1

Korzystając z twierdzenia Pitagorasa otrzymujemy:

(AB)² = 7² + 1²

(AB)² = 49 + 1 = 50

AB = √50

Wyłączamy czynnik przed pierwiastek (przypomnienie TUTAJ)

AB = 5√2