Trójkąt równoboczny - wysokość i pole

Jak to zrobić

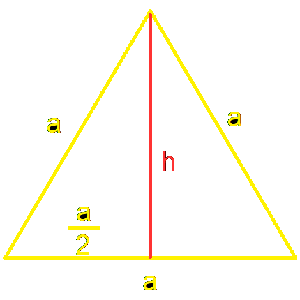
Spójrzmy na trójkąt prostokątny, który powstał na lewo od wysokości.

Zgodnie z Twierdzeniem Pitagorasa:

(½a)² + h² = a²

¼a² + h² = a²

h² = ¾a²

Obustronnie pierwiastkując otrzymujemy wzór na wysokość trójkąta równobocznego:

h =	a√3
	2

Podstawiamy wysokość do wzoru na pole trójkąta

P =	1	⋅ a ⋅ h =	1	⋅ a ⋅	a√3
	2		2		2

Otrzymujemy wzór na pole trójkąta równobocznego:

P =	a2√3
	4

Przykład 1:

Jeśli bok trójkąta równobocznego ma długość 60 cm, to wysokość:

h =	60√3	= 30√3
	2

Natomiast pole:

P =	602√3	=	3600√3	= 900√3
	4		4

Przykład 2:

Jeśli pole trójkąta równobocznego ma 4√3, to bok trójkąta możemy obliczyć podstawiając tę wartość do wzoru na pole:

4√3 =	a2√3
	4

Obustronnie mnożąc przez 4 i dzieląc przez √3, otrzymujemy:

a² = 16

a = 4