Twierdzenie Pitagorasa

Jak to zrobić

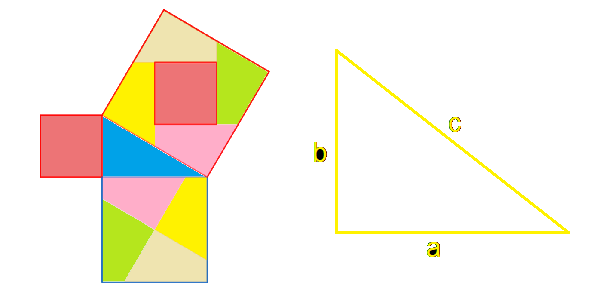
To jedno z najważniejszych i niewątpliwie najsłynniejsze twierdzenie geometryczne.

Jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.

a² + b² = c²

Prezentacja

Czewonym suwakiem można zmieniać długość pionowej przyprostokątnej; niebieskim - ustawić dowolny moment animacji, a klikając START u uruchamia się animację.

Przykład 1

Oblicz długość przeciwprostokątnej, jeśli przyprostokątne mają długości 3 cm i 4 cm

3² + 4² = c²

9 + 16 = c²

c² = 25

c = 5 cm

Przykład 2

Jedna z przyprostokątnych ma 4 cm długości, a przeciwprostokątna ma 6 cm. Oblicz długość trzeciego boku.

a² + 4² = 6²

a² + 16 = 36

a² = 20

a = √20

Wyłączamy czynnik przed pierwiastek (przypomnienie TUTAJ )

a = 2√5

Ćwiczenie

Oblicz długość przeciwprostokątnej, jeśli przyprostokątne mają długości i

c = √ = √

Oblicz długość przyprostokątnej, jeśli przeciwprostokątna ma długość , a druga przyprostokątna:

a = √ = √